|
|
|
|
| La modernité |
| Psychanalyse |
| H. de Campo |
| L'infini |
| Math_Méta |
| La postérité |
| B. Pascal |
|
|
La quadrature du cercle : une recherche métaphysique de Nicolas de Cues.
N. de Cues est un philosophe qui n’hésite pas à mettre à l’épreuve un principe philosophique - la coïncidence des opposés - pour en tester la validité dans une science - en l’occurrence, les mathématiques. Le défi est audacieux et suffisamment rare pour mériter d’être étudié. Malheureusement, les textes mathématiques de N. de Cues n’ont pas encore été vraiment travaillés. Tous les commentateurs s’accordent à dire que les mathématiques sont essentielles dans sa philosophie et, pourtant, très peu se sont avisés d’aller vraiment lire ses oeuvres mathématiques. Ou lorsque ces derniers en parlent, ils passent très vite sur le détail des démonstrations (Par exemple, Nagel, Fritz, Nicolaus Cusanus und die Enstehung der exakten Wissenschaften, (Münster Westfalen : Aschendorff, 1984), Buchreihe der Cusanus, Gesellschaft, Band IX, et Schulze, Werner, Zahl, Proportion, Analogie. Eine Untersuchung zur Metaphysik und Wissenschaftshaltung des Nikolaus von Kues , (Münster Westfalen : Aschendorff, 1978), Buchreihe der Cusanus-Gesellschaft, Band. VII).
Il est vrai que ce sont des textes difficiles à déchiffrer (De Transmutationibus geometricis, De Arithmeticis complementis, De circuli Quadratura, De Quadratura circuli, De quadratura circuli (Magister Paulus ad Nicolaum Cusanum), De Mathematicis complementis, Declaratio rectilineationis curvae, De Una recti curvique mensura, De sinibus et chordis, De caesarea circuli quadratura, De mathematica perfectione, De mathematicis aurea propositio). Joseph Ehrenfried Hofmann (Nikolaus von Kues, Die mathematische Schriften, traduction et notes par Josepha et Joseph Ehrenfried Hofmann, Hamburg, Félix Meiner Verlag, 1951) a donné une première édition allemande en 1951. On doit en reconnaître la très grande qualité d’établissement du texte et de la traduction, mais on peut y trouver aujourd’hui quelques insuffisances. Quand le propos est un peu elliptique ou compliqué, Hofmann introduit des incises, voire des explications dans le texte ; certes, toute traduction est une interprétation, mais elle ne doit pas être une explication ; celle-ci doit seulement faire l’objet éventuel de notes. Hofmann introduit dans le texte même de sa traduction un symbolisme tout à fait étranger aux mathématiques de l’époque, par exemple, le symbole de la racine√ qui est une invention postérieure, ou l’écriture de proportions sur le modèle ab : bc = bc : cd, ou if2 : bf2 avec l’écriture du carré en exposant. Ces anachronismes trahissent le texte, car si N. de Cues avait connu cette notation, il aurait été en possession des concepts qui l’accompagnent et sa compréhension des problèmes aurait été différente. Enfin, dans ses notes, Hofmann vérifie les propositions de N. de Cues par des fonctions trigonométriques que celui-ci ignorait totalement. Certes, il peut être intéressant de mesurer l’écart entre les connaissances d’un auteur et ce que nous savons aujourd’hui, mais l’essentiel est d’essayer de comprendre les raisons de cet écart, à partir des outils de l’époque. Il est vrai que ses démonstrations peuvent nous paraître bien maladroites. Mais il ne faut pas oublier que N. de Cues ne disposait ni du symbolisme algébrique, ni de l’analyse géométrique, ni du calcul fonctionnel, ni de la trigonométrie. Ses démonstrations reposent uniquement sur des rapports proportionnels, comme dans l’Antiquité.
On comprendra que cette partie essentielle de l’œuvre de Nicolas de Cues connaisse à nouveau une actualité : nous attendons pour cette année la parution des Mathematische Schriften, par le Professeur Menso Folkerts (Je renouvelle mes remerciements au professeur Menso Folkerts (Institut für Geschichte der Naturwissenschaft, Munich) qui m’a grâcieusement procuré le texte latin des trois oeuvres mathématiques du Cusain découvertes par Raymond Klibansky), dans l’édition scientifique de Heidelberg (Nicolai de Cusa opera omnia iussu et auctoritate Academiae Litterarum Heidelbergensis ad codicum fidem edita, Heidelbergae, 1931, sqq), et Monsieur Jean-Michel Counet vient de publier une profonde étude sur le rôle des mathématiques dans la philosophie de Nicolas de Cues (Counet, Jean-Michel, Mathématiques et dialectique chez Nicolas de Cuse, Paris, Vrin, 2000). Nous nous proposons dans cet article d’exposer quelques étapes caractéristiques des travaux mathématiques du Cusain et d’en indiquer la perspective métaphysique.
1 - Le projet de Nicolas de Cues
N. de Cues n’est pas un sceptique ; il a confiance dans les pouvoirs de l’esprit humain, mais à condition de distinguer la raison et l’intelligence. La raison ne peut saisir l’essence des choses, mais l’intelligence qui réside en nous, et qui est la marque de Dieu en nous, peut nous la faire voir. Grâce à notre intelligence, nous pouvons même nous approcher d’une vision de Dieu, une vision sans intermédiaire, une véritable intuition mystique. La raison procède laborieusement par abstractions successives, utilise des représentations approchantes, tente d’établir une adéquation entre ses concepts et ses objets, sans jamais parvenir à l’exactitude, alors que l’intelligence saisit d’un coup, par une intuition d’une puissance incomparable, ce qu’elle veut voir.
Parmi les limites de la raison, il en est une, essentielle, qui tient à son principe de fonctionnement : c’est le principe de non-contradiction. Lorsqu’elle se met à enquêter sur des objets métaphysiques comme Dieu ou l’infini, la raison tombe sur des antinomies qui l’empêchent d’aller plus loin ; elle refuse d’outrepasser son principe logique de non-contradiction. Pour qu’il y ait progrès dans la connaissance métaphysique, il faut que la raison discursive s’efface et accepte une rupture de l’intelligence avec la logique. En Dieu, les contraires sont réunis. Dieu est la synthèse de toutes choses, même des contradictoires : ... Il est manifeste d’après ce qui précède que Dieu embrasse tout, même les contradictoires (De Docta Ignorantia, L.I, 22, Herder, I, 270 : ... ex prioribus manifestum est Deum esse omnium complicationem, etiam contradictoriorum ... ( Nous nous référons pour nos citations des oeuvres autres que mathématiques au texte latin de l’édition établie par Dietlind et Wilhelm Dupré : Nikolaus von Kues, Die philosophisch-theologischen Schriften, Sonderausgabe zum Jubiläum, lateinisch-deutsch, 3 vol. , Wien, Herder, 1989), que nous signalerons en abrégé « Herder »)). Étant avant toutes choses, Dieu est au-dessus de toute affirmation comme de toute négation. L’étude de Dieu échappe aux principes de la logique qui, s’ils sont contraignants pour la raison, ne le sont plus pour l’intelligence, et l’intelligence qui admet la compatibilité des contraires, grâce à la fameuse coïncidence des opposés, va nous permettre d’approcher Dieu. Cette coïncidence des opposés est bien autre chose qu’une simple concession ; c’est véritablement un postulat fondamental et en même temps une méthode, une arme redoutable qui sert à résoudre quantité de problèmes : j’essaie de voir si par hasard cette difficulté pourrait prendre fin par le moyen des coïncidences, comme dans d’autres sciences. Je prétends qu’elle est d’une puissance maximale (De Mathematicis Complementis, L. I., Opera, 1004 : ... tentare coepi, si forte haec difficultas possit medio coincidentiarum finem capere, uti in aliis scientiis : vim illam maximam esse comperi). Elle n’est pas une pure négation du principe de non-contradiction, mais elle en est le dépassement nécessaire en cas de besoin. C’est grâce à l’union des contraires que l’intelligence va pouvoir comprendre les choses, car ce principe est inscrit dans les choses mêmes.
On peut déplorer un certain flottement dans la notion d’opposés qui recouvre trois catégories d’oppositions : 1 - l’opposition de l’actif et du passif (voir/être vu, aimer/être aimé, etc.) ; 2 - l’opposition du principe et du développé (l’unité/le nombre, le repos/le mouvement, l’éternité/le temps, etc.) ; 3 - l’opposition des contraires (fini/infini, lumière/obscurité, vertu/vice, etc.). On peut s’étonner de ces fluctuations, mais il importe de bien comprendre que ces oppositions sont bien plus fortes que celle des contradictoires. Pour N. de Cues, la contradiction relève seulement de l’ordre du discours ; c’est un principe de la dialectique qu’il considère comme une technique simplement verbale. La contradiction est une détermination interne à la raison discursive. Or, il prétend dépasser les mots pour dire l’être. Les oppositions sont des oppositions réelles.
Pour donner une idée de cette connaissance obtenue par l’intelligence, Nicolas de Cues utilise l’exemple des mathématiques. Il observe que les mathématiques, sciences rigoureuses qu’on ne peut suspecter d’irrationalisme, connaissent elles-mêmes une transmutation de leurs lois lorsqu’elles abordent l’infini. Tant que l’on demeure dans le domaine des figures finies, les mathématiques sont rationnelles et s’appuient sur le principe de non-contradiction ; dès que l’on infinitise les figures, les mathématiques deviennent intellectuelles et sont amenées à pratiquer la coïncidence des opposés.
Dans La Docte Ignorance (De Docta Ignorantia, I, 13, Herder, I, 236), il distingue trois mathématiques : la mathématique sensible (par exemple dans l’arpentage), la mathématique rationnelle (au premier chef, la géométrie euclidienne) et la mathématique intellectuelle. Le passage de l’une à l’autre s’effectue par une transsomption. La première transsomption consiste à porter une figure sensible finie jusqu’à sa limite maximale ; on porte ses propriétés à l’infini et l’on constate alors une coïncidence des opposés ; par exemple, on s’aperçoit que la circonférence du cercle infini coïncide avec la droite infinie ; la deuxième transsomption consiste à dépasser la figuration mathématique vers l’infini théologique, pour contempler l’infini lui-même, qui, bien entendu, est infigurable. La mathématique intellectuelle est donc une sorte de métamathématique qui propose des solutions nouvelles aux problèmes classiques grâce à une infinitisation.
Le problème le plus indiqué pour mettre à l’épreuve la coïncidence des opposés sera celui de la quadrature du cercle, puisqu’il s’agit de faire coïncider deux figures opposées, un cercle et un carré.
|
Qui enim circuli quaesiverunt quadraturam coincidentiam circuli et quadrati in aequalitate praesupposuerunt, quae certe in sensibilibus non est possibilis. Non enim dabile est quadratum, quod non sit inaequale omni dabili circulo in materia. Hanc igitur aequalitatem, quam praesupposuerunt, non viderunt oculis carneis, sed mentalibus, et nisi fuerunt eam in ratione ostendere, sed, quia ratio non admittit coincidentias oppositorum, defecerunt. Coincidentia autem quaeri debuit intellectualitet in circulo eo, qui in omni polygonia est aequalis ... (Complementum theologicum, chap. IV, Herder, III, 662) |
Ceux en effet qui ont cherché la quadrature du cercle ont présupposé la coïncidence du cercle et du carré dans l’égalité, laquelle n’est assurément pas possible au niveau sensible. Car il n’existe pas de carré qui ne soit inégal à n’importe quel cercle engagé dans la matière. Cette égalité, qu’ils ont présupposée, ils ne l’ont donc pas vue avec leurs yeux physiques, mais avec leurs yeux mentaux, et s’ils ont essayé de la démontrer par le raisonnement, ils ont cependant échoué, puisque la raison n’admet pas la coïncidence des opposés. C’est intellectuellement qu’ils auraient dû chercher la coïncidence dans ce cercle qui est égal dans chaque polygone (Complément théologique, in N. de Cues, Trois traités sur la docte ignorance et la coïncidence des opposés, trad. F. Bertin, Paris, Cerf, 1991, 100-101). |
L’objectif de Nicolas de Cues, dans ses textes mathématiques, consiste tout simplement à réussir la quadrature du cercle en utilisant le principe de la coïncidence des opposés, et à démontrer ainsi la puissance et la fécondité de ce principe.
2 .1. Les Transmutations géométriques
Il se lance dans cette aventure intellectuelle à partir de 1445. Il écrit son premier ouvrage mathématique, les Transmutations géométriques dans lesquelles il « transmue » une figure en une autre à partir de quelques propositions simples. Le titre nous renvoie à l’alchimie. Bien qu’il ne semble guère en avoir eu la pratique, N. de Cues accordait peut-être une certaine valeur à l’alchimie, parce qu’elle renversait la théorie aristotélicienne de la séparation des formes en genres et espèces. La transmutation bousculait la physique d’Aristote (
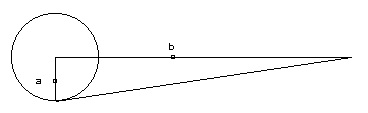
Viano, Cristina, « Aristote et l’alchimie grecque : la transmutation et le modèle aristotélicien entre théorie et pratique », Revue d’histoire des sciences, XLIX/2-3 (1996), 189-213), et promettre des transmutations géométriques, c’était dépasser la logique péripatéticienne. Cependant, le terme de transmutatio avait au Moyen Âge un sens plus large qu’il ne faut pas réduire aux seules opérations de l’alchimiste. La première proposition de ce livre sera le point de départ de toutes les discussions ultérieures [Fig. 1. Voir les figures plus bas]|
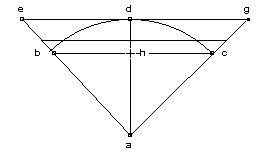
Semidiameter circuli isoperimetri trigono inscripto, se habet ad lineam a centro circuli cui trigonus inscribitur, ad quartam lateris ductam, in porportione sesquiquarta. Sit circulus super a centro descriptus, cui bcd trigonus inscribitur, diviso bc latere in quatuor partes aequales per efg signatas : dico si de a ad e linea ducta, protendatur per quartam sui ut fit ah, illam fore semidiametrum circuli, cuius circumferentia aequatur tribus trigoni lateribus (De transmutationibus geometricis, Opera, 946. (Nous nous référons à l’exemplaire imprimé de ses Opera, édité à Bâle par Henri Pétri en 1565, en deux volumes.) |
Le demi-diamètre du cercle isopérimétrique au triangle inscrit se rapporte à la ligne menée du centre du cercle, auquel le triangle est inscrit, au quart de son côté, en proportion des cinq quarts. Soit le cercle décrit autour du centre a, dans lequel est inscrit le triangle bcd ; tu divises le côté bc en quatre parties égales que tu marques par e, f, g ; je dis que, si on allonge la ligne menée depuis a vers e par son quart, ce qui fait comme ah, celle-ci sera le demi-diamètre du cercle dont la circonférence égale les trois côtés du triangle. |
On dessine un triangle équilatéral ; on trace son cercle inscrit et son cercle circonscrit ; on marque le point e au quart du côté du triangle, au milieu de bf ; le rayon ah du cercle de même périmètre que le triangle sera le segment tracé du centre a, passant par e égal aux 5 quarts de ae. N. de Cues ne démontre pas cette proposition, et, malheureusement, cette dernière comme celles qu’il en tire sont fausses ou infondées. Très rapidement, il s’aperçoit qu’il peut mieux faire que ses transmutations (), et pendant quatorze ans, au long d’une douzaine de traités, il va persévérer dans sa recherche d’une quadrature du cercle.
2.2. La méthode des isopérimètres
Parmi les diverses méthodes auxquelles il s’essaie, la plus caractéristique est la méthode des isopérimètres. Partant d’un triangle équilatéral, pris comme polygone régulier le plus simple, il augmente progressivement le nombre de côtés des autres polygones réguliers isopérimétriques - de périmètres égaux -, passant au carré, au pentagone, à l’hexagone, etc. Il trace pour chaque polygone son cercle inscrit et son cercle circonscrit. Le principe de la démonstration est le suivant : dans les polygones réguliers et isopérimétriques, variant du triangle au carré, etc., la différence de surface entre le cercle inscrit et le cercle circonscrit est extrême dans le triangle, puis s’amenuise dans le carré, etc., jusqu’à un cercle final que l’on peut définir comme le polygone possédant une infinité de côtés. Dans ce cercle isopérimétrique, on peut considérer que le cercle inscrit et le cercle circonscrit coïncident. Selon N. de Cues, il suffirait de déterminer la proportion entre tous les cercles inscrits et circonscrits, au moyen de leurs rayons, pour trouver l’égalité entre le périmètre d’un carré et celui d’un cercle. Une telle proportion illustrerait la fécondité du principe de coïncidence des opposés.
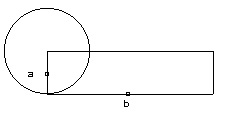
Voyons une des principales constructions que l’on trouve dans un petit traité de 1450 [Fig. 2 et 3] :
|
Faciemus autem hanc partem tibi hoc modo clariorem. Ex ab linea in tres partes divisa, c d e, triangulus designetur, & in eius latere cd signetur pars quarta ab quae fit ik, quae quadretur, & fit iklm : Describantur inscripti & circumscripti circuli ; & fit inscripti trigono semidiameter fg, & circumscripti fh, & inscripti tetragono ng, circumscripti no. Signetur deinde linea fh, & in eius medio g. Lineis de fgh tractis quantumlibet, trahatur ad fh aequidistans tn, cuius medium fit aa, & signetur semidiameter inscripti alicuius polygoniae isoperimetrae, puta tetragonae, quae fit np, & semidiameter circumscripti, quae fit no, & trahe de g per p in infinitum, & similiter de h per o lineam in infinitum & ubi ille concurrunt signa q, trahe per q aequidistantem ad fh, quae fit sr, in cuius medio signa bb. Dicimus rq esse semidiametrum circuli quaesiti, & eius circumferentiam aequalem ab lineae rectae (De Quadratura Circuli, Opera, 1095 : Est etiam nunc ars completa Geometricarum transmutationum, quam ante maius ... Maintenant, encore, l’art des transmutations géométriques est complet, plus qu’avant ...) |
Nous allons te rendre cette partie plus claire de la façon suivante. Avec la ligne ab divisée en trois parties, on dessine le triangle c,d,e. Sur son côté cd, on reporte en traçant ik, un quart de la droite ab ; de là, on construit le carré iklm. On dessine les cercles inscrits et circonscrits ; soit fg le demi-diamètre du cercle inscrit dans le triangle, fh celui du circonscrit ; soit ng celui du cercle inscrit dans le carré, no celui du circonscrit ; on trace ensuite la ligne fh, et sur son milieu on marque le point g. On tire à partir de f, g, h, des lignes de longueur quelconque, puis, à équidistance de fh, on tire tn dont le milieu est aa ; ensuite, on marque le demi-diamètre du cercle inscrit à un polygone isopérimétrique quelconque, par exemple un carré, soit np, et le demi-diamètre du circonscrit, no. On tire de g par p une ligne à l’infini, et de même de h par o une ligne à l’infini. On note q le point où elles concourent. Puis on tire par q à équidistance de fh la ligne sr, au milieu de laquelle on note bb. Nous affirmons que rq est le demi-diamètre du cercle cherché, dont la circonférence est égale à la droite ab. |
Il faut lire successivement les deux figures. Sur la figure 2, avec la ligne ab divisée en trois parties égales, on dessine le triangle équilatéral c,d,e. Sur son côté cd, on reporte en traçant ik, un quart de la droite ab ; de là, on construit le carré iklm. On dessine les cercles inscrits et circonscrits à ces deux polygones. La figure 3, tirée de la précédente, représente une induction à partir du triangle et du carré : on tire à partir de f, g, h, des lignes horizontales de longueur quelconque, puis, parallèlement à fh, on tire tn dont le milieu est aa ; fg représente le rayon du cercle inscrit dans le triangle et fh celui du cercle circonscrit ; ensuite, on reporte sur tn le rayon du cercle inscrit au carré, soit np, et no, le rayon de son cercle circonscrit. Puis, N. de Cues procède à son induction : il tire de g par p une droite à l’infini, et de même de h par o une droite à l’infini. Il note q le point où elles concourent. Il tire par q parallèlement à fh la ligne sr. Il affirme que rq est le rayon du cercle cherché dont la circonférence est égale à la droite ab.
N. de Cues se trompe lorsqu’il ne trouve entre ces rayons qu’un seul genre de proportion, à savoir la proportion « droite ». Il exclut une variation « courbe ». Il croit que les rayons des cercles inscrits aux polygones isopérimétriques, ainsi que les rayons des cercles circonscrits aux mêmes polygones, croissent et décroissent en proportion continue. On peut s’étonner de ce qu’il n’ait pas entrevu son erreur, facilement repérable sur de simples figures. Il suffit de dessiner les cercles inscrits et circonscrits à des polygones réguliers isopérimétriques comme un triangle, un carré, puis un pentagone et un hexagone, par exemple, pour voir que la différence entre les rayons ne diminue pas régulièrement. Mais N. de Cues croit que grâce à des rapports proportionnels simples, on peut établir des variations uniformes, et par là, que ces variations peuvent toujours être représentées par des droites.
En 1453, il reçoit une lettre de son ami florentin Paolo Toscanelli qui lui signale son erreur :
|
Sed non video cur duae lineae hb & bd concludentes omnes illos excessus primarum & secundarum, non possent esse curvae omni genere curvitatis, & tunc non procederet demonstratio : erit enim illud quod in decima tua conclusione dixisti, quod primae capaciorum erunt semper maiores, & secundae minores (De quadratura circuli, Magister Paulus ad Nicolaum Cusanum, Opera, 1100). |
Mais je ne vois pas pourquoi les deux lignes hb et bd enfermant tous ces excès des premières et des secondes (Les premières sont les rayons des cercles inscrits ; les secondes sont les rayons des cercles circonscrits), ne peuvent pas être des courbes de tout genre de courbure, et alors la démonstration n’aboutirait pas : il se produirait en effet ce que tu as dit dans ta dixième conclusion, à savoir que les premières des surfaces seront toujours plus grandes et les secondes toujours plus petites. |
Nicolas de Cues reprend l’objection : Mais s’il n’est pas vrai que la droite passe ainsi, mais que, d’aventure, une courbe de quelque courbure passe de la première du triangle par les premières de tous les polygones jusqu’à la première du cercle, alors cette invention n’est pas suffisante (De Mathematicis complementis, L. I.,Opera, 1027. Sed si hoc non est verum, quod recta sic transeat, sed forte curva aliqua curvitate transeat de prima trigoni, per primas omnium polygoniarum ad primam circuli : tunc haec inventio non est sufficiens.) Mais il n’y répond pas ; il poursuit sa fausse route.
Il reçoit alors en cadeau du pape Nicolas V une nouvelle traduction des oeuvres d’Archimède, réalisée par Jacob de Crémone (La traduction des oeuvres d’Archimède fut commandée par Nicolas V à Jacob de Crémone ; elle fut terminée à la fin de l’été 1450 ; elle fut ensuite copiée et corrigée par Regiomontanus en 1462. Selon Clagett, N. de Cues n’a pas pu avoir accès à cette traduction, ni à ses sources avant cette année 1453) ; au lieu de lui faire reconsidérer la difficulté du problème, sa lecture d’Archimède le conforte dans son ambition scientifique. Le contraste est saisissant entre la morale intellectuelle de La docte ignorance, au sens où elle est un appel à l’humilité face au savoir, et cette persistance à vouloir réussir là où Archimède avait échoué.
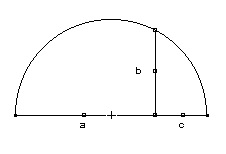
2.3. L’association d’Archimède et de Bradwardine
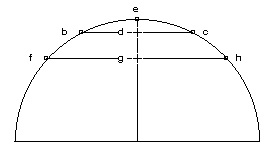
A partir de 1453, la référence à Archimède devient prédominante dans ses textes mathématiques. Le raisonnement par l’absurde archimédien du type « si A n’est pas plus grand que B et si B n’est pas plus grand que A, alors A et B sont égaux » lui paraît très proche de son principe de coïncidence des opposés, puisqu’il s’agit de réduire la différence entre deux termes opposés en apparence pour les réunir dans une égalité. Constamment, il conduit ses démonstrations géométriques avec le raisonnement archimédien. Il utilise deux instruments mathématiques : la première proposition du traité De la mesure du cercle d’Archimède et les paragraphes de la section 4 de la troisième partie de La géométrie spéculative de Bradwardine. C’est en associant ces deux références qu’il pense avoir trouvé une nouvelle proportion entre le droit et le courbe. Avec une singulière constance, à travers quelques variantes, il répète la même démonstration en quatre endroits différents de ses textes mathématiques (De Quadratura circuli, De Mathematicis complementis, L.I., De Una recti curvique mensura, De sinibus et chordis). La proposition d’Archimède énonce que tout cercle est équivalent à un triangle rectangle dans lequel l’un des côtés de l’angle droit est égal au rayon du cercle et la base (c’est-à-dire l’autre côté de l’angle droit) égal au périmètre du cercle (Archimède, La mesure du cercle, trad. Charles Mügler (Paris : Belles Lettres, t. I., 1970), 138) [Fig. 4]. N. de Cues transforme légèrement cette proposition en remplaçant le triangle rectangle par un rectangle dont la largeur est égale au rayon du cercle et la longueur est égale à la demi-circonférence du cercle, ce qui va de soi [Fig. 5.]. Le rectangle issu de la multiplication du demi-diamètre par la demi-circonférence du cercle n’est ni plus grand ni plus petit que l’aire du cercle (De Mathematicis complementis, L.I., prop. 7., Opera, 1011 : Quadrangulus surgens ex multiplicatione semidiametri in semiperipheriam circuli: nec maior nec minor est area circuli).
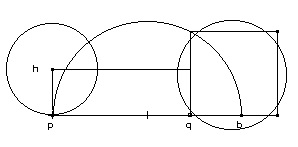
Il s’agit alors de chercher la longueur du côté c du carré de même surface que celle du rectangle. Si l’on y parvient, on aura effectivement atteint la quadrature du cercle. Pour y parvenir, N. de Cues utilise sa lecture de Bradwardine pour trouver comment entre deux lignes droites se tiennent deux moyennes en proportion continue (De transmutationibus geometricis, Troisième prémisse, Opera, 962 : quomodo inter duas lineas rectas, duae mediae continue proportionales statuantur). Bradwardine s’exprime ainsi : Deux lignes droites étant données qui sont jointes directement en une ligne droite, si on décrit un demi-cercle sur toute la ligne ainsi composée et agrégée des deux, la ligne qui s’élève perpendiculairement de la limite commune aux deux lignes jointes jusqu’à la circonférence sera la moyenne entre les lignes données selon une proportionnalité continue (Bradwardine, Thomas, Geometrica speculativa, latin text and english trad. George Molland (Stuttgart : éd. Steiner, 1989), Partie III, proposition 3. 4. 4., inspirée elle-même de Euclide, Les Eléments, VI, 13) Soit un demi-cercle sur le diamètre duquel on dresse une demi-corde à angle droit. On sait que la grande portion du diamètre est à la demi-corde ce que la demi-corde est à la petite portion du diamètre : a/b = b/c. Ce dispositif permet de construire le carré de même surface qu’un rectangle donné en introduisant son côté dans une proportion continue entre la largeur et la longueur du rectangle. La construction finale part d’un cercle et aboutit à un carré [Fig. 6.]. On obtient en élevant sur q le côté du carré de même périmètre que le cercle, que l’on peut reproduire en le superposant sur le carré [Fig. 7.].
L’ennui, c’est que cette habile construction repose sur une pétition de principe. En effet, si Archimède affirme que tout cercle est équivalent à un triangle rectangle dans lequel l’un des côtés de l’angle droit est égal au rayon du cercle et la base (c’est-à-dire l’autre côté de l’angle droit) égal au périmètre du cercle, il ne dit aucunement comment transformer la circonférence du cercle en ligne droite. Or, Nicolas de Cues prend cette ligne pour donnée alors que c’est justement cette transformation qu’il s’agit de démontrer. Il admet au départ de sa démonstration ce qu’il cherche à construire.
2.4. La vision intellectuelle
De la perfection mathématique date de 1458. N. de Cues considérait cet ouvrage comme son meilleur traité mathématique, un peu comme le point d’orgue de sa recherche. Il y introduit une nouvelle notion, la visio intellectualis (Le thème de la vision est constant chez N. de Cues. La même année, il rédige le De Beryllo : il imagine un « béryl » pour l’intelligence, une sorte de loupe mentale pour percevoir la vérité invisible). Il semble avoir renoncé définitivement à déterminer exactement, par des procédés purement rationnels, l’égalité de la droite et de la courbe. Il recourt donc à l’intuition. Il part de la coïncidence de l’arc le plus petit et de la corde la plus petite, aperçue par une vision intellectuelle, puis il utilise ce rapport pour les grandeurs intermédiaires [Fig. 8.]
|
Intentio est ex oppositorum coincidentia, Mathematicam venari perfectionem. Et quia perfectio illa plaerumque consistit in rectae curvaeque quantitatis adaequatione : propono habitudinem duarum rectarum linearum, se ut chordam ad suum arcum habentium, investigare : sciens illa habita, me medium habere curvam quantitatem cum recta adaequandi. Et quoniam ad has inveniendas necesse est, me alicuius chordae ad arcum habitudinem scire : ut ex illa cognita pergere queam ad artem. Sed quomodo est possibile, me cuiusquam datae chordae ad arcum habitudinem scire : cum inter illas quantitates adeo contrarias forte non cadat numerabilis habitudo ? Necesse erit igitur me recurrere ad visum intellectualem, qui videt minimam sed non assignabilem chordam, cum minimo arcu coincidere. Nam quanto chorda minor, tanto sagitta adhuc minor : ut de sagitta chordae bc, minor est quam ge sagitta chordae fh, quia bc minor fh, & ita consequenter. Minima igitur chorda, qua minor dari non potest, si assignabilis foret non haberet sagittam, & ita etiam non foret minor arcu suo. Coincideret igitur ibi chorda & arcus, si ad minimam quantitatem in talibus deveniretur. Hoc probe videt intellectus necessarium, licet sciat, nec arcum nec chordam (cum sint quantitates) esse simpliciter minimas in actu & posse, cum continuum fit semper divisibile. Ad hauriendam autem scientiam habitudinis, respicio ad intellectualem visionem, & dico me videre ubi est chordae & arcus aequalitas : scilicet in simpliciter minimo utriusque (De Mathematica Perfectione, Opera, 1110). |
Mon but est d’arriver à la perfection mathématique par la coïncidence des opposés. Et parce que cette perfection consiste pour tout dans l’égalité en quantité de la droite et de la courbe, je propose de chercher le rapport de deux lignes droites se tenant dans le rapport de la corde à son arc : connaissant ce rapport, j’obtiens un moyen d’égaliser la quantité courbe avec la droite. Et puisqu’il est nécessaire de les trouver, je connaîtrai le rapport de n’importe quelle corde à l’arc pour, ce rapport étant connu, progresser dans cet art. Mais comment est-il possible de connaître le rapport de n’importe quelle corde donnée à son arc, puisqu’entre ces quantités tellement contraires par hypothèse, il n’y a pas de rapport calculable ? Il me sera donc nécessaire de recourir à la vision intellectuelle, qui voit que la corde minima mais inassignable coïncide avec l’arc minimum. De fait, plus la corde est petite, plus la flèche est petite. Comme la flèche de de la corde bc est plus petite que la flèche ge de la corde fh, parce que bc est plus petite que fh, et ainsi de suite. Donc, la plus petite corde telle qu’on ne peut en donner de plus petite, si elle était assignable, n’aurait pas de flèche, et ainsi ne pourrait être plus petite que son arc. Il y aurait là coïncidence de la corde et de l’arc, si on en arrivait à leur quantité minimale. Il est nécessaire que l’intellect voie bien cela et il lui est permis de le savoir : ni l’arc ni la corde - en tant que quantités - ne peuvent être simplement les plus petits en acte et en puissance, puisque le continu est toujours divisible. Pour parvenir à la connaissance de leur rapport, je me tourne vers la vision intellectuelle, et je dis que je vois où est l’égalité de la corde et de l’arc, à savoir simplement dans le minimum de chacun des deux. |
Au lieu de raisonner sur l’infiniment grand comme dans la Docte Ignorance, il raisonne désormais sur l’infiniment petit qu’il voit intellectuellement. Mais il lui faut justifier cette nouveauté. La vision intellectuelle procède de la certitude métaphysique : elle instaure une nécessité en essence. Elle abroge la notion de quantité au profit d’une idée particulière de l’égalité des grandeurs. Elle porte sur des grandeurs absolues, en minimum et en maximum, au-delà de la mesure quantitative, et donc sur des figures insensibles et parfaites. Elle ne fait plus la différence entre le petit et le grand, puisque le minimum et le maximum sont vus « pareillement ». Dans le sensible, le petit et le grand sont relatifs et sont comparables, donc mesurables, alors que dans l’insensible absolu, il n’y a ni augmentation, ni diminution. Il suffirait donc de s’appuyer sur les propriétés de ces deux extrêmes que sont le minimum et le maximum pour en déduire les propriétés des dimensions intermédiaires. Il est évident que l’aspect mystique de la vision interfère, ici, dans une recherche mathématique dont la finalité, ne l’oublions pas, est de conduire d’une certaine manière à Dieu.
2.5. La proposition d’or
La proposition d’or dans les mathématiques est le dernier texte mathématique connu de N. de Cues. Il date du 8 Août 1459 et contient les mêmes idées que la Perfection mathématique, avec, toutefois, un effort de fondation mathématique rigoureuse. Le Cusain revient à son idée d’origine, à savoir la rectification de la circonférence à l’infini. Sa proposition est la suivante : dans un quadrant, le rapport des sections de rayons à la ligne qui les détermine est constant, que cette ligne soit une corde, un arc ou une tangente [Fig. 9.].
(ab+ad+ac)/arc bdc = (ab+ah+ac)/corde bhc = (ae+ad+ag)/tan edg;
|
Sive tres lineae a centro egressae angulos aequales semirectos aut minores constituentes per arcum seu chordam terminentur, eandem ad terminantem tenent habitudinem. Uti si de a, centro bdc, indiffinitae quantitatis lineae egrediantur, duos aequales circa a angulos semirectos seu minores constituentes per alicuius circuli arcum, puta bdc, aut eius chordam, scilicet bhc, sive contingentem, puta edg, terminentur : eandem teneant tres lineae ab, ad et ac ad arcum terminantem habitudinem quam ab, ah et ac ad bhc terminantem sive ae, ad et ag ad edg terminantem. Quod idem est ac si diceretur : Sicut bdc arcus est quadrans et tres lineae ab, ad et ac sunt tres semidiametri eius, sic edg est aequalis alicui quadranti et ae, ad et ag aequantur tribus semidiametris circuli eius (Aurea propositio in mathematicis, texte découvert par R. Klibansky, inédit). |
Si, du centre a de bdc, on tire les lignes ab, ad et ac d’une longueur indéfinie, et constituant sur a deux angles égaux demi-droits ou plus petits, ces angles sont fermés par un arc de cercle quelconque, par exemple bdc, ou par sa corde bhc, ou par la tangente edg. Les trois lignes ab, ad et ac ont le même rapport à l’arc de délimitation que les lignes ab, ah et ac ont à la corde de délimitation bhc, ou que les lignes ae, ad et ag ont à la tangente edg. On dira que c’est la même chose : puisque l’arc bdc est un quadrant dont les trois lignes ab, ad et ac sont les trois demi-diamètres, alors edg, de même, est égale à un quadrant, et ae, ad et ag sont ensemble comme les trois demi-diamètres de son cercle. |
L’idée générale de cette proposition est que, quel que soit l’angle de la portion de cercle considéré, et donc, quelle que soit la courbure de l’arc, les trois rapports sont constants. Par exemple, si l’arc s’aplatit vers la corde, la diminution du rayon au centre de l’arc est compensée par l’allongement des deux rayons à ses extrémités. Inversement, si la courbure de l’arc s’accentue, l’allongement du rayon au centre de l’arc est compensée par le raccourcissement des deux rayons à ses extrémités. Ainsi le rapport (ab+ad+ac)/ arc bdc reste constant. Cette proposition intuitive n’est appuyée sur aucun calcul.
Toutes ces tentatives n’apportent aucune découverte mathématique. Nous le savons aujourd’hui. N. de Cues ne pouvait pas savoir à son époque que le problème de la quadrature du cercle était impossible. Mais ce n’est pas une raison pour jeter ses travaux dans l’oubli. Nous avons à les apprécier avec justice. S’il a si longtemps persisté dans son entreprise, ce n’est pas par ignorance, ou par incompétence. Nous formulons l’hypothèse d’un sens métaphysique précis à ses recherches que nous pourrons entrevoir si nous nous posons ces trois questions :
- Comment peut-il imaginer qu’on puisse trouver une proportion régulière entre les différents polygones isopérimétriques ? C’est la question du rôle des proportions.
- Comment peut-il imaginer qu’une égalité soit possible entre un cercle et un carré ? C’est la question de l’égalité entre deux grandeurs de genres différents.
- Pourquoi privilégie-t-il la ligne droite sur la ligne courbe ? C’est la question de la nature des objets géométriques.
3. 1. La théorie des proportions
Comment N. de Cues pouvait-il croire qu’une proportion régulière existait entre les différents polygones isopérimétriques ? Pour le comprendre, il faut rappeler l’importance historique de la théorie des proportions. En effet, avant la conceptualisation de la notion de fonction, les mathématiciens du Moyen Âge latin ne disposaient que de la proportion. Le problème philosophique fondamental de la proportion est celui des structures de la connaissance : la proportion n’est-elle qu’un ordre conçu par la pensée pour se représenter les choses ou est-elle un ordre inscrit dans les choses mêmes ? Pour les platoniciens, la proportion n’est pas qu’un simple instrument de représentation du monde. C’est un lien dans les choses mêmes, un lien tel que ces choses se tiennent ensemble et d’une diversité forment un seul tout.
Héritier du Moyen Âge, N. de Cues en reprend tous les problèmes et, fatalement, les confusions. La proportion a la puissance d’un dogme, à cette époque ; il n’est donc pas étonnant que ce concept s’enfle en compréhension comme en extension, jusqu’à devenir monstrueux. Le règne universel de la proportion ou de l’analogie - les deux termes deviennent alors synonymes - permet de surmonter toute diversité, voire toute contrariété dans une unité de rapports. N. de Cues connaît surtout la proportion continue a/b =b/c qui permet des raisonnements du style : si a/b = b/c et si b/c = c/d, alors a/b = c/d. La plupart de ses démonstrations sont menées avec ce raisonnement.
La proportio est, selon lui, la clé essentielle de la recherche : Toute recherche consiste en une proportion comparative facile ou difficile, et c’est pourquoi l’infini qui échappe, comme infini, à toute proportion, est inconnu. Or, la proportion qui exprime accord en une chose d’une part et altérité d’autre part, ne peut se comprendre sans le nombre. C’est pourquoi le nombre enferme tout ce qui est susceptible de proportions (De Docta Ignorantia, I, 1, Herder, I, 194). Le domaine privilégié dans lequel se déploie la puissance de la proportion sera le domaine mathématique : Nous appelons symboliquement nombre la première réalité dérivée, parce que le nombre est le substrat de la proportion ; sans nombre il n’est, en effet, aucune proportion (De Mente, 6, Herder, III, 524). La raison en est que Dieu lui-même l’a utilisée lors de la création : Dieu s’est servi, dans la création du monde, de l’arithmétique, de la géométrie, de la musique et de l’astronomie, tous arts dont nous faisons usage aussi quand nous recherchons les proportions des choses, des éléments et des mouvements (De Docta Ignorantia, II, 13, Herder, I, 410). C’est pourquoi on la retrouve partout dans le monde : La proportion est le lieu du monde, ou la région de la forme, et la matière le lieu de la proportion (De Mente, 6, Herder, III, 520). Il est clair que, pour N. de Cues, la proportion n’est pas seulement un instrument de la pensée. La proportion est la loi du monde.
Dans ses textes mathématiques, il use abondamment du mot medietas, qui désigne la médiété dans l’expression medietas duplae (la médiété double). Il connaît la notion de médiété géométrique, qu’il appelle medium proportionale. Il parle aussi de continue proportio pour la proportion continue. Il lui arrive de préciser qu’une proportion est rationnelle (rationalis proportio), mais quand il utilise le mot ratio, c’est au sens de la cause, de la raison d’un fait, et non pour désigner un rapport. Pour parler d’un rapport, il emploie constamment le terme habitudo qui peut recouvrir indifféremment les concepts de relation, de médiété ou de proportion. Il n’utilise pas le terme de proportionalitas, mais seulement l’adjectif proportionalis (ou improportionalis).
Revenant sans cesse comme un leitmotiv, la disproportio est ce qui caractérise la relation du fini et de l’infini : finiti ad infinitum nulla est proportio. Or, de fait, la quadrature du cercle consiste bien à chercher une proportion entre des grandeurs finies et un infini. Il y aurait donc une incohérence fondamentale dans l’entreprise du Cusain, incohérence dont il n’a pas eu conscience, car si la disproportion entre la petitesse de l’homme et l’infinie grandeur de Dieu est évidente, celle qui se trouve entre une grandeur finie et un infiniment petit est beaucoup moins évidente. N. de Cues ne parle pas de disproportion dans le problème de la quadrature du cercle. Il n’y voit que la difficulté à trouver des rapports intermédiaires entre le carré et le cercle.
Il appelle comparatio l’opération propre à l’esprit qui cherche une proportion : Tous ceux qui recherchent jugent de l’incertain, en le comparant à un présupposé certain par un système de proportions. Toute recherche est donc comparative, et elle use du moyen de la proportion : si l’objet de la recherche se laisse comparer au présupposé par une réduction proportionnelle peu étendue, le jugement d’appréhension est aisé ; mais si nous avons besoin de beaucoup d’intermédiaires, alors naissent la difficulté et la peine. Cela est bien connu dans les mathématiques (De Docta Ignorantia, I, 1, 36-37, Herder, I, 194 : Omnes autem investigantes in comparatione praesuppositi certi proportionabiliter incertum iudicant ; comparativa igitur est omnis inquisitio, medio proportionis utens. Ut dum haec, quae inquiruntur, propinqua proportionali reductione praesupposito possint comparari, facile est apprehensionis iudicium ; dum multis mediis opus habemus, difficultas et labor exoritur ; uti haec in mathematicis nota sunt ...). Cette multiplicité d’intermédiaires est bien, en effet, ce qui préoccupe N. de Cues dans le problème de la quadrature du cercle.
Pour trouver ces proportions, il construit de nombreux tableaux comparatifs qui soutiennent ses raisonnements, comme, par exemple, celui qui compare des rayons de cercles circonscrits à un triangle et à un hexagone [Fig. 10].
|
Constat autem quoniam habitudo lateris hexagoni, ad semidiametrum circuli circumscripti trigono isoperimetro, in quadratis nota est, cum quadratum dg si est 4 quadratum lateris hexagoni isoperimetri (quoniam est medietas chordae subtensae tertiae parti circumferentiae eiusdem circuli) est ut tria : notum est consequenter, ed quadratum. Quoniam si quadratum dg est 4 quadratum ed est 9 cum dg fit duplum ad ge. Sic erit fe nota, quia est latus hexagonicum, cuius quadratum est ut tria, in habitudine qua quadratum dg est ut 4 erit similiter ecsic nota. Sic erunt lineae ed & ef notae. Et quoniam trianguli egl & ecn sunt aequianguli latera eandem tenent proportionem. Eadem ergo est proportio ge ad el, quae est ce ad en (De Arithmeticis Complementis, Opera, 992). |
Il est aussi évident que le rapport du côté de l’hexagone au demi-diamètre du cercle circonscrit au trigone isopérimétrique est connu dans les carrés ; si le carré de dg est 4, le carré du côté de l’hexagone isopérimétrique (parce qu’il est la moitié de la corde sous-tendue de la troisième partie de la circonférence du même cercle) est égal à trois : on connaît par conséquent le carré de ed. Parce que si le carré de dg est 4, le carré de ed est 9 et dg fait le double de ge. Ainsi, fe sera connu, parce qu’il est un côté de l’hexagone, dont le carré est comme trois, dans le rapport par lequel le carré de dg est comme 4 ; ec sera ainsi connu de la même façon. Les lignes ed et ef seront connues. Et parce que les triangles egl et ecn sont d’angles égaux, leurs côtés se tiennent en même proportion. Cette proportion est donc celle de ge à el, qui est celle de ce à en. |
Or, la notion de proportion suppose résolue la question de l’égalité, puisque toute proportion est une égalité de rapports.
3. 2. La question de l’égalité
Comment donc N. de Cues conçoit-il l’égalité ? Et surtout, comment peut-il affirmer qu’une égalité soit possible entre une figure rectiligne et une figure courbe ? Quelle importance accorde-t-il à ce que nous appelons l’exigence d’homogénéité entre les grandeurs qu’il nous faut respecter pour pouvoir parler d’égalité ?
Pour évaluer son niveau d’information sur cette délicate question, il peut être utile de considérer ce que l’on pouvait comprendre de l’axiome d’Eudoxe (La définition 1 d’Eudoxe au début du livre V des Eléments d’Euclide pose qu’ une grandeur est partie d’une grandeur, la plus petite de la plus grande, quand elle mesure la plus grande. trad. B. Vitrac (Paris, P.U.F., 1990), tome II, 35), à l’époque, car c’est cet axiome d’Eudoxe qui définit le concept d’égalité. Les auteurs du XIVème siècle étaient très au fait de la difficulté (Citons, par exemple, Duns Scot, Thomas Bradwardine, Nicole Oresme, Grégoire de Rimini). Par exemple, Campanus de Novare l’expose assez clairement ; mais l’ennui, c’est qu’il ajoute aux postulats d’Euclide ses propres postulats dont il pense qu’ils sont des conditions nécessaires (Ainsi le postulat d’existence d’une quatrième proportionnelle : Autant quelque quantité est de même genre qu’une autre quantité, autant il y en a une troisième pour une quatrième du même genre. D’après Murdoch, John E., The medieval language of proportions : elements of the interaction with greek foundations and the development of new mathematical techniques, in Symposium on the history of science, (Oxford University : 1961)).
Dans sa quadrature du cercle du 12 Juillet 1450, N. de Cues affirme qu’on peut déterminer l’égalité entre un carré et un cercle : On peut donner un carré plus grand pour un cercle donné - plus grand, cependant pas d’une partie aliquote de ce carré ; et on peut donner un carré de telle sorte qu’il soit un carré plus proche encore du cercle, au point qu’aucun ne sera plus proche et qu’aucun ne sera plus petit d’une partie aliquote du cercle (La quadrature du cercle du 12 Juillet 1450, texte découvert par R. Klibansky, inédit. Tali quidem modo dici potest, dato circulo posse dari quadratum, quod etsi fuerit maius circulo, non tamen aliqua parte aliquota eius, scilicet quadrati ; et dato quadrato potest dari circulus minor eo, non tamen minor parte aliquota circuli. Et consequenter ex hoc habetur, quod licet dato circulo possit dari quadratum maius, non tamen parte aliquota eius maius ; et quod quocumque quadrato tali dato adhuc possit dari aliud praecisius circulo, licet nullum praecisissimum, et nullum minus circulo parte aliquota eius...). Et pour être bien compris, il déclare : Et je tiens ce point de vue pour le plus vrai. Mais il sait que cette égalité entre des lignes de genres différents est très discutée. Il distingue clairement deux cas de non-proportionnalité : d’une part, l’incommensurabilité (par exemple entre la diagonale et le côté du carré, parce qu’on arrive à une fraction irrationnelle) ; d’autre part, ce que nous appelons l’hétérogénéité (par exemple entre l’angle d’incidence (On entend par angle d’incidence, au Moyen Âge, l’angle formé par l’intersection d’un arc et d’une droite, à l’intérieur de l’arc. On le distingue de l’angle de contingence qui est formé par l’intersection d’un arc et d’une droite, à l’extérieur de l’arc, autrement dit, qui est compris entre l’arc et la tangente) et l’angle rectiligne, parce qu’il n’y a aucune partie aliquote de l’un permettant de mesurer l’autre). Mais il introduit une nouvelle notion, très fragile, celle de « la ligne la moins non-proportionnelle ». Cette ligne la moins non-proportionnelle ne sera pas celle qui s’approche au plus près de l’égalité arithmétique, mais sera celle qui, au-delà du numérique et de l’hétérogène, parvient à une égalité dont il pose l’existence comme nécessaire. Il y a là, bien entendu, un coup de force métaphysique de sa part. Il s’autorise du postulat de l’existence d’une quatrième proportionnelle de Campanus pour affirmer, malgré tout, une sorte d’égalité entre le droit et le courbe. Passer d’une non-proportionnalité relative à l’affirmation de l’existence d’une proportion déterminée est bien le fait d’un glissement de sens, d’un manque de rigueur dans le raisonnement. On peut peut-être y voir aussi la marque de la pratique fréquente de la théologie négative (La théologie négative est une tradition remontant au Pseudo-Denys l’Aréopagite consistant à ne parler de Dieu qu’avec des négations) : quand on ne peut définir positivement une notion, on passe par le procédé indirect de l’impossibilité de sa négation. Mais ce qui est admissible dans des cas nettement définis grâce au principe du tiers-exclu, ne peut fonctionner dans des cas relatifs définis par une simple négation. Parler d’une grandeur la « moins non-proportionnelle » à une autre ne permet pas de dire que ces deux grandeurs soient égales.
L’assimilation que le Cusain semble opérer entre le raisonnement archimédien et son principe de la coïncidence des opposés manifeste également une confusion. Le raisonnement archimédien repose très clairement sur le principe de non-contradiction (deux grandeurs ne peuvent être inégales et égales en même temps), alors que la coïncidence des opposés est un dépassement de ce principe. Il y aurait là encore une incohérence dans l’entreprise du Cusain : il aspire à une mathématique intellectuelle alors qu’il se sert d’instruments de la géométrie rationnelle.
On voit donc comment la métaphysique vient au secours des mathématiques. Quand il ne peut déterminer exactement le rapport entre l’arc minimum et la corde minimum, N. de Cues fait appel à une vision intellectuelle qui saisit une égalité entre des grandeurs au-delà du quantifiable. Quand il a besoin d’une égalité entre des grandeurs non-proportionnelles, il pose l’existence d’une quatrième proportionnelle au-delà du numérique et de l’hétérogène. Ses « solutions » mathématiques sont commandées par des choix métaphysiques.
3. 3. - La nature des objets mathématiques
Enfin, pourquoi N. de Cues privilégie-t-il la ligne droite sur la ligne courbe ? Ce choix relève d’une hiérarchie entre les objets géométriques. La question de cette hiérarchie nous conduit de nouveau à rechercher les sources métaphysiques du Cusain, recherche délicate, tant l’essence des objets mathématiques est discutée à l’époque. Pour aller au plus vite, on doit situer N. de Cues dans le courant néoplatonicien du XVème siècle. Il s’inspire plus ou moins directement de Proclus, auteur d’un Commentaire du premier livre des Eléments d’Euclide (Proclus, Commentaire sur le premier livre des Eléments d’Euclide, trad. Paul Ver Eecke (Paris : Blanchard, 1940). Cependant, un problème de chronologie se pose. En effet, le texte grec de cette oeuvre a été imprimé pour la première fois à Bâle par Simon Grynaeus en 1533, et la traduction latine a été réalisée par Francis Barozzi à Padoue en 1560, près d’un siècle après la mort du Cusain. Comment aurait-il pu le lire ? Il possédait d’autres œuvres de Proclus. Le commentaire du Parménide de Platon était son livre de chevet. Aurait-il reconstitué par lui-même la classification des lignes, à la lecture des autres œuvres de Proclus ? C’est peu probable. Néanmoins, les copies manuscrites des œuvres de Proclus circulaient abondamment au XVème siècle. Bessarion avec lequel Nicolas de Cues était très lié possédait plusieurs de ces copies. Il est vraisemblable que c’est par là que le Cusain a pu méditer sur la classification proclusienne des lignes géométriques).
On trouve dans le néoplatonisme du Cusain, trois concepts primordiaux : - le développement (explicatio) qui est la descente progressive de l’Un vers la multiplicité ; - l’enveloppement (complicatio) qui est la remontée de l’être vers l’Un, car, dès qu’il reconnaît son être véritable, l’être qui était descendu cherche à revenir vers la sphère supérieure en se dépouillant de l’enveloppe étrangère qui recouvrait son être propre ; - la hiérarchie, qui est la succession de degrés et d’ordres entre les êtres.
Nous proposons le schéma suivant, résultant de la lecture des textes du Cusain - en particulier, le De Mente, chapitres 7, 9 et 10 -, pour exposer sa distribution des objets mathématiques. Cette distribution qui s’opère entre les deux ordres de l’infini et du fini est bien évidemment d’origine théologique.
Il est évident que chaque objet mathématique est aussi un objet métaphysique. Il faut commencer par la définition de la limite (qui n’est pas un être, mais un principe qui intervient dans l’engendrement des êtres) car le point, la ligne et la surface sont des limites (le point pour la ligne, la ligne pour la surface et la surface pour le volume). La fonction de la limite est d’empêcher que la grandeur étendue ne s’échappe dans l’indétermination, qu’elle s’étende dans l’infini. La limite est ce qui retient l’être dans la dispersion. Aussi, ce qui limite est-il inférieur d’une dimension à ce qui est limité. Par exemple, la ligne, qui n’a qu’une dimension, limite la surface plane qui en a deux. Bien que les limites participent aux formes qu’elles limitent, elles gardent leurs raisons en elles-mêmes et ne les reçoivent pas des choses limitées. Ainsi, le point limite la ligne et s’y trouve, mais il ne reçoit pas son principe de la ligne. La ligne se définit par le point et non l’inverse. Cette fonction de la limite est stratégique dans une théorie de l’enveloppement des objets : chaque être qui cause d’autres êtres est cause du tout de ces êtres. La cause, non seulement détermine, mais enveloppe ce qu’elle cause.
On entrevoit très vite comment ces définitions métaphysiques induisent une hiérarchie entre les objets. Ainsi, pour les lignes, la ligne droite et la ligne circulaire ont des caractères qui en font des symboles très différents. La ligne droite est la plus simple ; nulle dissimilitude ne s’y trouve. La ligne droite est symbole de la Providence inflexible, incorruptible, immaculée, inépuisable, omnipotente, présente à toutes les choses (Proclus, Commentaire sur le premier livre des Éléments d’Euclide, trad. Paul Ver Eecke, 98), écrit Proclus. La ligne circulaire est plus composée : on y trouve le concave et le convexe, images de la transformation. La ligne circulaire est symbole de l’énergie qui se contracte sur elle-même, qui se ramasse en elle-même, et qui soumet toute chose à une délimitation intelligible.
Pour N. de Cues, la ligne droite est essentiellement l’image d’un développement, l’expression géométrique la plus claire du développement de Dieu dans le monde. Il faut prendre la ligne, non comme le trait, mais comme le tracé, c’est-à-dire comme ce qui se meut à partir de soi. Lorsque N. de Cues parle de ligne droite, il entend, en fait, un segment de droite qui peut toujours se prolonger en glissant sur lui-même ; c’est une conception très concrète, très pratique de l’objet géométrique ; il faut voir sur la ligne droite la règle toujours prête à coulisser sur le trait, toujours prête à guider le crayon pour dérouler les points. Une ligne droite n’est donc jamais tout à fait délimitée, finie. Pour N. de Cues, la ligne circulaire est l’image de l’être parfait auquel rien ne manque, c’est une image de Dieu - entendons ici l’image au sens pédagogique et non comme une théophanie -. L’image est produite par la pensée dans son effort de compréhension des choses. La ligne infinie est circulaire, puisque dans une telle figure le principe coïncide avec la fin (De Docta Ignorantia, II, 12, Herder, I, 396 : ... tunc est circularis ; nam ibi principium coincidit cum fine), et il précise : Dans le cercle, qui ne contient ni commencement ni fin, je vois l’image de l’éternité (De Ludo Globi, Herder, III, 234-236 : In circulo enim, ubi non est principium nec finis (...) video imaginem aeternitatis). La ligne droite et la ligne circulaire sont donc deux images de la divinité, avec cette différence : la rectitude symbolise la puissance de Dieu qui s’étend dans le monde, car la ligne droite procède d’un mouvement ouvert et illimité, le point de départ se tenant dans un écart croissant vis-à-vis de lui-même ; la circularité symbolise l’être de Dieu qui se tient identique à lui-même, car la ligne circulaire est fermée, chaque point de la ligne maintenant un écart constant par rapport au centre.
Face à ces deux images de la nature divine que sont le droit et le circulaire, qu’est-ce qu’une ligne courbe non-circulaire ? Le courbe est conçu comme une altération, comme une dégradation, notamment parce que la courbure est finie. Le circulaire est rangé du même côté que le droit grâce à son infinité alors que le courbe est rejeté du côté du fini, comme un moindre être.
|
Scitur ex mathematicis rectum non dici nisi secundum modum unum. Una enim linea recta sive magna sive parva non est magis aut minus recta quam alia. Rectitudo igitur infinita esse concipitur, quia non clauditur quantitate, nec recipit magis et minus. Absoluta igitur rectitudo est infinita. Curvitas autem non potest esse infinita. Quapropter circularis linea circuli infiniti non potest esse curva, quia infinita. Clauditur igitur omnis curvitas terminis magnitudinis suae. Et non habet curvitas exemplar nisi rectitudinem. Qui enim depingere vult curvam lineam respicit mente ad rectam, et cadere eam facit ab illa reflexe. Curvitas autem, quae est infinitae rectitudini propinquior, similitudo est circularis curvitatis. Infinita enim rectitudo est ipsa aeternitas, quae non habet principium, nec medium, nec finem, nec quantitatem, nec qualitatem. Circularis autem curvitas, quae necessario est quanta et composita habet coinidentiam principii et finis et est necessario a rectitudine infinita tamquam a principio suo et veritate sua. Curvitas enim ex se non est, sed ab illa rectitudine est, quae est eius mensura. Rectum enim mensurat curvum. Cadit igitur circularis curvitas a rectitudine infinita perfectiori modo quam non circularis, quia sicut rectitudo infinita caret principio, medio et fine. Sic in curvitate circulari illa coincidunt et minime distant seu differunt. Unde plus assimilatur circularis curvitas infinito quam finita rectitudo, ubi principium, medium et finis distant (Complementum theologicum, chap. VII, Herder, III, 672).
|
On sait grâce aux mathématiques que la rectitude ne se prédique qu’en un sens univoque. Car une ligne droite, qu’elle soit grande ou petite, n’est ni plus droite ni moins droite qu’une autre ligne droite. On conçoit donc la rectitude comme infinie, puisqu’elle n’est pas limitée par la quantité et qu’elle n’admet ni le plus ni le moins. La rectitude absolue est donc infinie. En revanche la curvitude ne peut pas être infinie. C’est pourquoi la ligne circulaire du cercle infini ne peut pas être courbe, puisqu’elle est infinie. Chaque courbure est donc bornée par les limites de sa grandeur. Et la curvitude n’a pas d’autre prototype que la rectitude. Que celui qui désire tracer une ligne courbe contemple mentalement la ligne droite et la fasse dériver de celle-ci en l’incurvant. Or la courbure, qui est la plus proche de la rectitude infinie est une image approximative de la courbure circulaire. Car la rectitude infinie est l’Eternité même, qui ne comporte ni commencement, ni milieu, ni fin, ni quantité, ni qualité. En revanche la courbure circulaire, qui est nécessairement quantifiée et composée, comporte la coïncidence du commencement et de la fin et procède nécessairement de la rectitude infinie comme de son principe et de sa vérité. La courbure en effet n’existe pas par elle-même, mais dérive de cette rectitude, qui est sa mesure. Car le droit mesure le courbe. La courbure circulaire dérive donc de la rectitude infinie sous un mode plus parfait que la courbure non circulaire, puisque de même que la rectitude infinie est dénuée de commencement, de milieu et de fin, de même ceux-ci coïncident dans la courbure circulaire et ne diffèrent ou ne se distinguent en rien les uns des autres. Par conséquent la courbure circulaire se rapproche davantage de l’infini que la rectitude finie, où le commencement, le milieu et la fin diffèrent les uns des autres (trad. F. Bertin, in Trois traités sur la docte ignorance (Paris : Cerf, 1991), 106-107). |
Cette hiérarchie relève de ce que A. Charles-Saget met en évidence dans L’architecture du divin, à propos des objets géométriques chez Proclus. Un des principes de classement de ces objets consiste à dire que le principe engendrant est plus riche que l’être engendré. Chez N. de Cues, cela signifie que la ligne droite est infinie, parfaite et éternelle, la ligne circulaire est infinie et parfaite, et la ligne courbe est finie seulement. On trouve un second principe : on reconnaît dans le caractère négatif des premières définitions le signe de la puissance des termes définis ; le point indivisible engendre la ligne divisible ; la ligne sans largeur engendre la surface. On parvient au principe fondamental de la théologie négative : « les négations engendrent les affirmations. » (Charles-Saget, Annick, L’architecture du divin : mathématique et philosophie chez Proclus (Paris : Belles-Lettres, 1982), 273), nous dit A. Charles-Saget. Chez N. de Cues, cela donne : la ligne droite n’a ni commencement, ni milieu, ni fin, ni quantité, ni qualité ; la ligne circulaire n’a ni commencement, ni milieu, ni fin, mais a une quantité et est composée ; enfin, la ligne courbe a un commencement, un milieu, une fin, une quantité et est composée. On est loin du classement moderne des lignes qui renversera complètement cette hiérarchie métaphysique. Képler - qui a lu N. de Cues - a fait du cercle un cas particulier des sections coniques : le cercle est une ellipse dont tous les diamètres sont égaux. Aujourd’hui, la ligne droite est considérée comme un cas particulier de la ligne courbe : c’est une ligne dont la courbure est nulle. Le principe générateur des lignes est maintenant la courbure, et non plus la rectitude.
La perspective mathématico-métaphysique de N. de Cues
Nous disposons maintenant d’un certain nombre d’éléments pour comprendre les cadres de la recherche du Cusain. Revenons, par exemple, à sa tentative par la méthode des isopérimètres [Fig. 3.]. Le point q est conçu comme la coïncidence du minimum (le rayon du cercle inscrit) et du maximum (le rayon du cercle circonscrit). Nous voyons que cette représentation mathématique est principalement nécessitée par des exigences métaphysiques : la ligne est pour N. de Cues, le développement (explicatio) du point ; ce développement, surtout s’il est déterminé par une proportion, sera nécessairement continu et régulier ; la coïncidence est le lieu de Dieu : c’est en Dieu que le maximum et le minimum sont réunis. Le point q est l’image la plus adéquate de Dieu. Quand N. de Cues évoque dans les Compléments mathématiques l’hypothèse effarante pour lui que, d’aventure, une courbe de quelque courbure passe de la première du triangle par les premières de tous les polygones jusqu’à la première du cercle (De Mathematicis complementis, L. I., Opera, 1027), il n’entend pas un simple degré de courbure, mais bien une ligne d’une autre nature ; « de quelque courbure » signifie « de quelque être courbe », c’est-à-dire relevant d’une nature dégradée par rapport au cercle et à la ligne droite. Si l’on admet que la coïncidence est le lieu de Dieu, que c’est en Dieu que le maximum et le minimum sont réunis, alors on mesure combien il était impossible pour le Cusain que la courbure puisse mener à Dieu ; il y a un empêchement métaphysique d’une telle gravité que la résolution du problème mathématique de la quadrature du cercle ne peut pas ne pas s’y plier.
Si N. de Cues ne réussit pas son expérimentation de la coïncidence des opposés en mathématiques, ce n’est pas par incompétence mathématique, mais parce qu’il y a une incompatibilité entre ce principe et la démonstration mathématique. S’appuyant sur les rapports entre les mathématiques et la métaphysique, il pense qu’il y a continuité entre les deux, que les mathématiques peuvent servir à la fois d’initiation et d’application à la métaphysique, et qu’en retour, certains principes métaphysiques peuvent l’aider à résoudre des problèmes mathématiques. L’enjeu de cet échec dépasse largement le cadre de la philosophie cusaine et prend une dimension épistémologique générale : il n’y a pas communauté d’objets et de démarches entre les deux disciplines. Cet échec est en même temps une preuve pour la docte ignorance : les hommes sont dans l’incapacité d’atteindre avec exactitude la vérité. Il resterait à savoir si les travaux du Cusain ont constitué une avancée dans l’approche continue de cette vérité. On peut légitimement en douter.
Au terme de cette étude, on découvre que ce n’est ni par ignorance, ni par maladresse que N. de Cues échoue. Le niveau de sa discussion est tout à fait remarquable, alors que les chercheurs de cette époque étaient privés des instruments nécessaires pour avancer dans le problème, par rapport aux acquis d’Archimède. Mais il y a à se demander pourquoi N. de Cues a tant persisté dans son entreprise, pourquoi il n’a pas vu qu’il ne pouvait pas résoudre son problème. Il faut comprendre son erreur « de l’intérieur », et étudier ses concepts métaphysiques comme autant d’obstacles épistémologiques internes. Cette étude se présente finalement comme l’archéologie d’un échec. Il est des échecs pitoyables, d’autres plus nobles. Il en est des glorieux. Il semble que ce philosophe qui a eu le courage de soumettre ses idées à l’épreuve des sciences n’échoue pas sans une certaine grandeur.
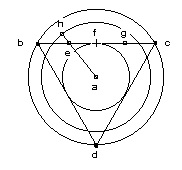
Fig. 1.
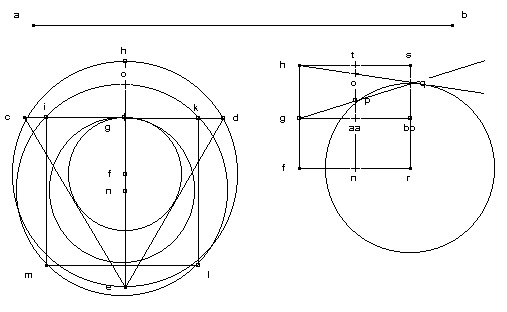
Fig. 2. Fig. 3.
|
Fig. 4. |
Fig. 5. |
|
Fig. 6. |
Fig. 7. |
|
Fig. 8. |
Fig. 9. |
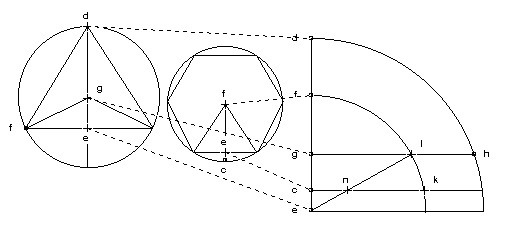
Fig. 10.
Bibliographie :
Nicolai de Cusa, Opera, (Bâle : Henri Pétri, 1565).
Nikolaus von Kues, Die mathematische Schriften, traduction allemande par Josepha Hofmann et commentaires par Joseph Ehrenfield Hofmann, (Hamburg : Félix Meiner Verlag, 1951).
Nikolaus von Kues, Die philosophisch-theologischen Schriften, Sonderausgabe zum Jubiläum, lateinisch-deutsch, 3 vol. , (Wien : Herder, 1989).
Nicolas de Cues, Trois traités sur la docte ignorance et la coïncidence des opposés, trad. F. Bertin (Paris : Cerf, 1991).
Bradwardine, Thomas, Geometrica speculativa, latin text and english trad. George Molland (Stuttgart : Steiner, 1989).
Charles-Saget, Annick, L’architecture du divin : mathématique et philosophie chez Proclus, (Paris : Belles-Lettres, 1982).
Counet, Jean-Michel, Mathématiques et dialectique chez Nicolas de Cuse, (Paris : Vrin, 2000).
Euclide, Les Eléments, trad. B. Vitrac (Paris : P.U.F., 1990).
Murdoch, John E., "The medieval language of proportions : elements of the interaction with greek foundations and the development of new mathematical techniques", in Symposium on the history of science, (Oxford University : 1961).
Proclus, Commentaire sur le premier livre des Eléments d’Euclide, trad. Paul Ver Eecke (Paris : Blanchard, 1940).
Viano, Cristina, Aristote et l’alchimie grecque : la transmutation et le modèle aristotélicien entre théorie et pratique, Revue d’histoire des sciences, XLIX/2-3 (1996), 189-213.
Outils bibliographiques :
Kleinen-Danzer, Cusanus-Bibliographie (1920-1961), Mitteilungen und Forschungsbeiträge der Cusanus-Gesellschaft, 1, (Mainz : Matthias Grünewald Verlag, 1961).
Danzer, Robert, Cusanus-Bibliographie, Fortsetzung (1961-1964) und Nachträge, Mitteilungen und Forschungsbeiträge der Cusanus-Gesellschaft, 3, (Mainz : Matthias Grünewald Verlag, 1963).
Vasquez, Mario, Cusanus-Bibliographie, 3. Fortsetzung (1967-1973) mit Ergänzungen, Mitteilungen und Forschungsbeiträge der Cusanus-Gesellschaft, 10, (Mainz : Matthias Grünewald Verlag, 1973).
Kaiser, Alfred, Cusanus-Bibliographie, 4. Fortsetzung (1972-1982) mit Ergänzungen, Mitteilungen und Forschungsbeiträge der Cusanus-Gesellschaft, 15, (Main : Matthias Grünewald Verlag, 1982).
Jean-Marie Nicolle