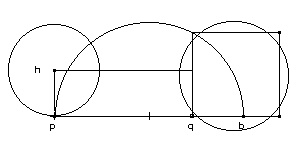La moyenne proportionnelle
Dans le De Mathematicis complementis, L.I., N. de Cues obtient la moyenne proportionnelle entre deux parties d’une droite afin de construire le carré isopérimétrique au cercle donné, grâce à un demi-cercle.
|
Partant d’un cercle avec son rayon, on construit le rectangle dont la longueur fait la demi-circonférence du cercle. Puis on cherche la moyenne proportionnelle grâce au demi-cercle construit sur la base du rectangle et l’on obtient par là le côté du carré de même périmètre que le cercle de départ, cercle que l’on reproduit sur le carré. Dans le De Quadratura Circuli de 1450, le cercle donné est tracé plus bas. |
|
Pour cela, il utilise deux références mathématiques : la première proposition du traité De la mesure du cercle d’Archimède et les paragraphes de la section 4 de la troisième partie de La géométrie spéculative de Bradwardine. C’est en associant ces deux références qu’il pense avoir trouvé une proportion entre le droit et le courbe. Avec une singulière constance, à travers quelques variantes, il répète la même démonstration en quatre endroits différents de ses textes mathématiques.
|
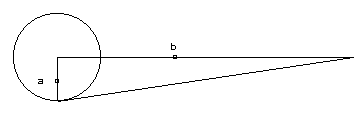
La proposition d’Archimède énonce que tout cercle est équivalent à un triangle rectangle dans lequel l’un des côtés de l’angle droit est égal au rayon du cercle et la base (c’est-à-dire l’autre côté de l’angle droit) égal au périmètre du cercle. ( Archimède, La mesure du cercle, trad. Charles Mügler, Paris, Belles Lettres, t. I., 1970, p. 138). a = rayon du cercle ; b = circonférence du cercle. |
|
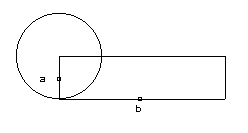
N. de Cues transforme légèrement cette proposition en remplaçant le triangle rectangle par un rectangle dont la largeur est égale au rayon du cercle et la longueur est égale à la demi-circonférence du cercle, ce qui va de soi.
|
La surface d’un cercle est égale à celle du rectangle formé par le demi-diamètre du cercle et la demi-circonférence. (De Mathematicis complementis, L.I.) |
|
Il s’agit alors de chercher la longueur du côté c du carré de même surface que celle du rectangle. Si l’on y parvient, on aura effectivement atteint la quadrature du cercle.
Pour y parvenir, N. de Cues utilise sa lecture de Bradwardine ( Bradwardine, Thomas, Geometrica speculativa, texte latin et traduction anglaise de George Molland, Wiesbaden-Stuttgart, Franz Steiner Verlag, 1989, Partie III, prop. 3.4.4 (inspirée elle-même d’Euclide)) pour trouver comment entre deux lignes droites se tiennent deux moyennes en proportion continue.
|
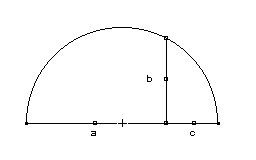
Soit un demi-cercle sur le diamètre duquel on dresse une demi-corde à angle droit. On sait que la grande portion du diamètre est à la demi-corde ce que la demi-corde est à la petite portion du diamètre : a/b=b/c. Ce dispositif permet de construire le carré de même surface qu’un rectangle donné en introduisant son côté dans une proportion continue entre la largeur et la longueur du rectangle. |
|
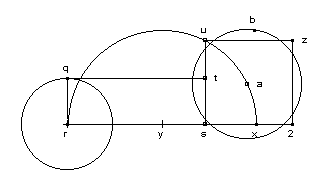
L’ensemble de cette démarche se trouve soutenue, alors, par cette figure :
|
|
rq est le demi-diamètre, rs la moitié de ab, soit la circonférence du cercle, rqts le rectangle égal au cercle, sx égale à rq, y le point au milieu de rx, et le centre du cercle ryx, su la moyenne proportionnelle entre rs et sx, d’après Euclide VI, 9, suz2 le carré qui est de même surface que le cercle de demi-diamètre rq (De Quadratura circuli ). On a donc le carré su2 égal au rectangle rq x rs ; su est construit par la propriété de Bradwardine, établissant la proportion continue entre une demi-corde et les deux portions du diamètre, soit, ici, entre et rs et sx.
Cependant, le défaut de toute cette démarche tient à ce qu'elle repose sur une pétition de principe : N. de Cues suppose donné - la longueur de la demi-circonférence du cercle - ce qu'il s'agit justement de chercher.