La méthode des isopérimètres
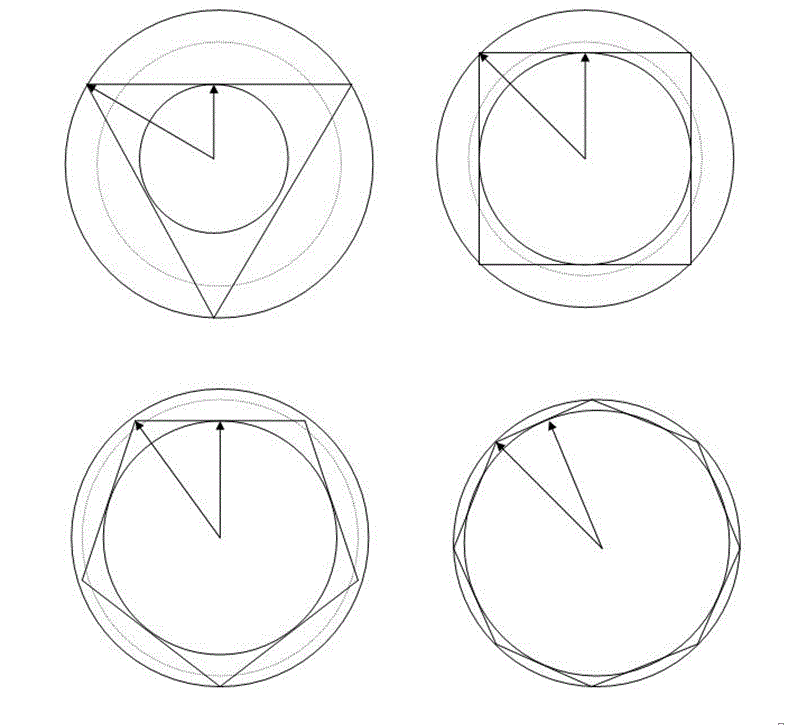
Parmi les diverses méthodes auxquelles le Cusain s’essaie, la plus révélatrice est la méthode des isopérimètres. Cette méthode consiste à comparer des figures de même périmètre, les isopérimètres : partant d’un triangle équilatéral, pris comme polygone régulier le plus simple, on augmente progressivement le nombre de côtés des autres polygones réguliers isopérimétriques, jusqu’au cercle, pour en chercher le demi-diamètre. Dans les polygones réguliers et isopérimétriques, variant du triangle au carré, etc. jusqu’au cercle, la différence de surface entre le cercle inscrit et le cercle circonscrit est extrême dans le triangle, puis s’amenuise dans le carré, etc., jusqu’au cercle. Dans le cercle, on peut considérer que le cercle inscrit et le cercle circonscrit coïncident. Selon N. de Cues, il suffit de déterminer la proportion entre ces cercles, au moyen de leurs demi-diamètres, pour trouver le rapport entre la surface d’un cercle et celle d’un carré.
|
|
La première proposition auquel il aboutit sera le point de départ de toutes les discussions ultérieures : Le demi-diamètre du cercle isopérimétrique au triangle inscrit se rapporte à la ligne menée du centre du cercle, auquel le triangle est inscrit, au quart de son côté, en proportion des cinq quarts. (Fig. 1, p. 83)
Ses démonstrations nous paraissent aujourd’hui bien maladroites. Mais il ne faut pas oublier que N.de Cues ne disposait ni du symbolisme algébrique, ni de l’analyse géométrique, ni du calcul fonctionnel, ni de la trigonométrie. Ses démonstrations reposent uniquement sur des rapports proportionnels, comme dans l’Antiquité. La méthode des isopérimètres revient essentiellement à chercher une proportion. Mais, le problème est que N. de Cues ne va pas - parce que c’est impossible - trouver une proportion satisfaisante. Voyons une des principales constructions que l’on trouve dans un petit traité de 1450 :
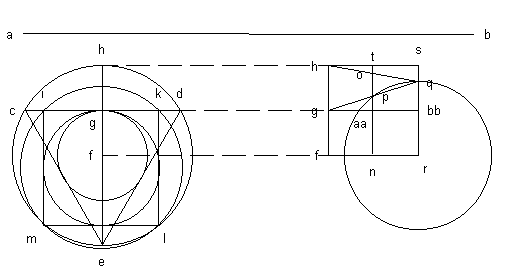 |
| Faciemus autem hanc partem tibi hoc modo clariorem. Ex ab linea in tres partes divisa, c d e, triangulus designetur, & in eius latere cd signetur pars quarta ab quae fit ik, quae quadretur, & fit iklm : Describantur inscripti & circumscripti circuli ; & fit inscripti trigono semidiameter fg, & circumscripti fh, & inscripti tetragono ng, circumscripti no. Signetur deinde linea fh, & in eius medio g. Lineis de fgh tractis quantumlibet, trahatur ad fh aequidistans tn, cuius medium fit aa, & signetur semidiameter inscripti alicuius polygoniae isoperimetrae, puta tetragonae, quae fit np, & semidiameter circumscripti, quae fit no, & trahe de g per p in infinitum, & similiter de h per o lineam in infinitum & ubi ille concurrunt signa q, trahe per q aequidistantem ad fh, quae fit sr, in cuius medio signa bb. Dicimus rq esse semidiametrum circuli quaesiti, & eius circumferentiam aequalem ab lineae rectae. De Quadratura circuli (1450) |
Nous allons te rendre cette partie plus claire de la façon suivante. Avec la ligne ab divisée en trois parties, on dessine le triangle c,d,e. Sur son côté cd, on reporte en traçant ik, un quart de la droite ab ; de là, on construit le carré iklm. On dessine les cercles inscrits et circonscrits ; soit fg le demi-diamètre du cercle inscrit dans le triangle, fh celui du circonscrit ; soit ng celui du cercle inscrit dans le carré, no celui du circonscrit ; on trace ensuite la ligne fh, et sur son milieu on marque le point g. On tire à partir de f, g, h, des lignes de longueur quelconque, puis, à équidistance de fh, on tire tn dont le milieu est aa ; ensuite, on marque le demi-diamètre du cercle inscrit à un polygone isopérimétrique quelconque, par exemple un carré, soit np, et le demi-diamètre du circonscrit, no. On tire de g par p une ligne à l’infini, et de même de h par o une ligne à l’infini. On note q le point où elles concourent. Puis on tire par q à équidistance de fh la ligne sr, au milieu de laquelle on note bb. Nous affirmons que rq est le demi-diamètre du cercle cherché, dont la circonférence est égale à la droite ab. |
Or, N. de Cues se prend lui-même au piège lorsqu’il ne trouve entre ces rayons qu’un seul genre de proportion, à savoir la proportion «droite». Il exclut une variation «courbe» dans les proportions. Il croit que les rayons des cercles inscrits aux polygones isopérimétriques, ainsi que les rayons des cercles circonscrits aux mêmes polygones, croissent et décroissent en proportion continue, alors qu’en réalité la proportion suit une fonction asymptotique vers l’infini. On peut s’étonner de ce qu’une telle fonction, facilement repérable sur de simples figures, n’ait pas été entrevue par N. de Cues. Il suffit de dessiner les cercles inscrits et circonscrits à des polygones réguliers isopérimétriques comme le triangle, le carré, puis un hexagone et un heptagone, par exemple, pour voir que la différence entre les rayons ne diminue pas régulièrement. Mais N. de Cues pense que grâce à des rapports proportionnels simples, on peut établir des variations uniformes, et par là, que ces variations peuvent toujours être représentées par des droites.
En 1453, il reçoit une lettre de son ami florentin Paolo Toscanelli qui lui signale son erreur : Mais s’il n’est pas vrai que la droite passe ainsi, mais que, d’aventure, une courbe de quelque courbure passe de la première du triangle par les premières de tous les polygones jusqu’à la première du cercle, alors cette invention n’est pas suffisante . Le plus étonnant est de lire dans la lettre de son ami Toscanelli l’indication claire de son erreur ; mais N. de Cues ne veut pas la voir ; il poursuit sa fausse route.