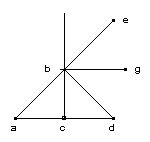Les Transmutations
Comment établir une égalité entre une ligne droite et une ligne courbe ? Nicolas de Cues s’attaque à ce problème dès son premier ouvrage mathématique intitulé Les Transmutations Géométriques, de 1445 ; c'est un ouvrage composé d’une façon tout à fait classique pour un traité mathématique. Dans l’introduction, N. de Cues donne des définitions, pose le problème général - comment établir un rapport proportionnel entre une courbe et une droite -, puis le subdivise en quatre questions pour le résoudre. Le titre - Les Transmutations - renvoie bien évidemment à l’alchimie. N. de Cues a passé quelques semaines, au printemps 1428, à Paris, avec son maître Heymeric de Campo, pour recopier des textes alchimiques attribués à R. Lulle (en réalité, de la main d’Arnaud de Villeneuve). Bien qu’il ne semble guère en avoir eu la pratique, N. de Cues accordait peut-être une certaine valeur à l’alchimie, en tant qu’elle renversait la théorie aristotélicienne de la séparation des formes en genres et espèces. La transmutation bouscule la physique d’Aristote. Promettre des transmutations géométriques, c’était donc dépasser la logique péripatéticienne.
Son objectif est de montrer la fécondité du principe de la coïncidence des opposés en géométrie. Il prétend avoir trouvé, grâce à ce principe qui s’appuie sur l’infinitisation des figures, l’art de convertir le courbe en droit, et réciproquement, et donc, il croit détenir la solution au problème de la quadrature du cercle. La première proposition sera le point de départ de toutes les discussions ultérieures :
Le demi-diamètre du cercle isopérimétrique au triangle inscrit se rapporte à la ligne menée du centre du cercle, dans lequel le triangle est inscrit, au quart de son côté, en proportion des cinq quarts .
|
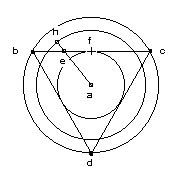
On dessine un triangle équilatéral ; on trace son cercle circonscrit et son cercle inscrit ; on marque le point e au quart du côté du triangle, au milieu de bf; Le rayon ah du cercle isopérimétrique au triangle sera le segment tracé du centre a, passant par e égal aux cinq quarts de ae. N. de Cues ne démontre pas cette proposition, mais il affirme qu’on peut déterminer par elle l’égalité entre un carré et un cercle : On peut donner un carré plus grand pour un cercle donné - plus grand, cependant pas d’une partie aliquote de ce carré; et on peut donner un carré de telle sorte qu’il soit un carré plus proche encore du cercle, au point qu’aucun ne sera plus proche et qu’aucun ne sera plus petit d’une partie aliquote du cercle . Et pour être bien compris, il déclare : Et je tiens ce point de vue pour le plus vrai. |
|
Avec cette proposition, N. de Cues se lançait, sans le savoir, dans une entreprise qui le dépassait quelque peu. Voici un exemple de transmutation d’un triangle en cône par un mouvement de rotation, donné dans le De Mathematicis complementis :
|
abc est un triangle, le côté ab décrivant un conique, et cb étant le demi-diamètre de la base. Tire la ligne ac en continu, et mène de b une ligne de sorte que tu fasses un triangle égal, qui est bdc. Il est manifeste, si ad reste fixe, le triangle abd tournant autour, qu’il résulte un rhombe des deux coniques égaux. Tire donc ab en continu, ce qui fait be comme ab : il est clair, si on fait la rotation comme avant, que la ligne be produit une surface triple de la surface de ab, et ae une surface conique quadruple de celle de ab. D’où, si tu élèves bd au milieu entre bd et be - cela fait bg -, il en résulte une surface double, avec bd une égale, et avec be une triple. Et toujours on arrive au milieu, quand on fait un angle droit avec le demi-diamètre de la base : et si on élève plus ou moins, on produit plus ou moins. |
|
|
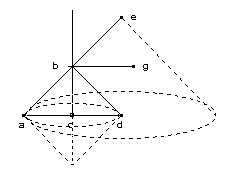
Manquant de la représentation en perspective, N. de Cues semble obscur dans sa construction. On peut comprendre le mouvement ainsi : Lorsque le triangle abc tourne autour de l'axe ce, ab décrit une surface conique. Lorsque le triangle abd tourne autour de l'axe ad, il forme un rhombe. Lorsque le triangle aed tourne autour de l'axe ed, ae décrit une surface conique quadruple de celle de ab. |
|