La proportion rectangulaire
Les Compléments Mathématiques sont le traité mathématique le plus volumineux de N. de Cues. Celui-ci a reçu au cours de l’année 1450 (ou 1453) la nouvelle traduction des oeuvres d’Archimède commandée par le pape Nicolas V à Jacob de Crémone. On peut supposer que la lecture de cette traduction a relancé ses recherches mathématiques. La première partie des Compléments date des premiers jours de Septembre 1453. Le texte est adressé au pape en remerciement pour la traduction en question.
N. de Cues commence par rappeler sa méthode des isopérimètres, puis se lance dans 14 propositions sur les propriétés des polygones et des cercles, largement inspirées d’Archimède et de Bradwardine. La principale proposition est la douzième et elle est longuement développée ; elle pose une proportion entre lignes droites et surfaces :
Si on pose l’excès de surface du cercle sur la surface du triangle comme la différence de la première et de la seconde lignes du triangle, alors l’excès de surface du cercle sur la surface des polygones intermédiaires entre le triangle et le cercle sera comme la différence entre sa première et sa seconde lignes .
La première ligne est le rayon du cercle inscrit au triangle. La seconde ligne est le rayon du cercle circonscrit. La différence entre les deux est appelée « flèche » par N. de Cues. La différence de surface entre divers polygones réguliers et leur cercle isopérimétrique serait donc proportionnelle à leur flèche.
Pour représenter cette proposition, N. de Cues imagine un tableau de proportions rectangulaire :
|
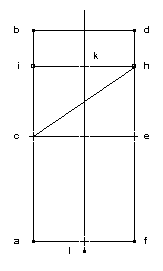
ac est la première ligne du triangle (rayon de son cercle inscrit) ; ab est la seconde ligne du triangle (rayon de son cercle circonscrit) ; eh = 2/3 cd ; ch exprime la croissance des rayons des cercles inscrits (par exemple, ml est le rayon de l’inscrit au quadrilatère) ; ih exprime la décroissance des flèches (par exemple, kh est la flèche du quadrilatère). |
 |
La variation est considérée comme rectiligne. C'est une erreur ...