Les tableaux de proportions

Les Compléments arithmétiques (De Arithmeticis complementis) paraissent en 1450 (mais ont pu être achevés dès la fin de 1445) et sont une réponse à une demande d’explication de la part de Paul Toscanelli sur la première proposition des Transmutations Géométriques ; il ne faut pas se laisser abuser par le titre : les Compléments Arithmétiques ne sont pas un texte d’arithmétique, mais bien de géométrie, dans lequel N. de Cues cherche une approximation de p . Le terme d’arithmétique ne vaut que pour désigner le nombre - une constante - permettant de calculer le rapport du diamètre à la circonférence du cercle. D’après lui, quel que soit le nombre de côtés du polygone, on obtient toujours le même rapport de proportionnalité entre les cordes et les arcs, et donc une valeur précise du rayon du cercle isopérimétrique aux polygones.

N. de Cues invente un instrument visuel pour comparer les rayons des cercles inscrits et circonscrits à divers polygones réguliers : c’est un quadrant qui va constituer une sorte de règle pour mesurer les proportions entre les polygones ; nous appellerons cet instrument dont nous retrouverons de nombreuses variantes « tableau de proportions », en référence à la définition de la géométrie comme projection de figures intérieures sur un tableau, ou sur le miroir intérieur de l’âme. (Cf. De Ludo Globi, p. 147, Herder, III, 322).

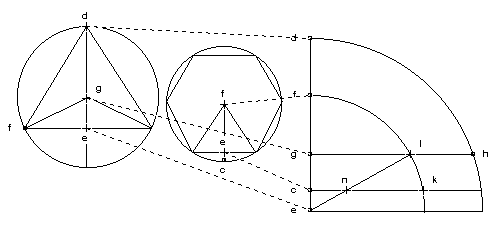
On reporte sur le côté vertical du quadrant les différents rayons :

dg est le rayon du cercle circonscrit au triangle;

ge est le rayon du cercle inscrit au triangle;

ef est le demi-côté du triangle;

cf est le rayon du cercle circonscrit à l’hexagone;

ef est le rayon du cercle inscrit à l’hexagone;

A partir de ce tableau, on peut tracer d’autres lignes permettant d’établir des proportions.