L'infinitisation
Démonstration de la coïncidence des opposés à l’infini, dans De la docte ignorance, Partie I, §§ 13 à 15. trad. L.Moulinier, Paris, éd. de la Maisne, 1979, pp.61-67.
Il s’agit pour N. de Cues de démontrer la validité de son principe de coïncidence des opposés à l’infini par l’infinitisation de figures géométriques. Le premier exemple, le plus célèbre, est celui de la rectification de la circonférence du cercle infini. N. de Cues donne d’abord sa proposition générale : s’il y avait une ligne infinie, elle serait une droite, elle serait un triangle, elle serait un cercle et elle serait une sphère. Puis il « démontre » chaque proposition.
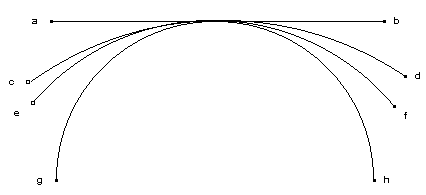 |
1. Une ligne infinie est une droite : Plus un cercle est grand, moins sa circonférence est courbe, et plus elle est une droite. Conclusion : la curvité de la ligne maxima est rectitude.
Les quatre propositions suivantes cultivent les paradoxes de l’infini :
2. La ligne infinie est un triangle, un cercle et une sphère.
3. La ligne infinie est le triangle maximum.
4. Le triangle maximum est un cercle.
5. La ligne infinie est une sphère.
2. La ligne infinie est un triangle, un cercle et une sphère :
|
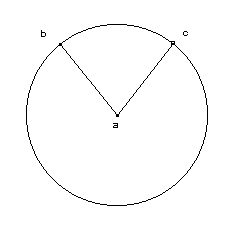
a. La ligne infinie est la plus longue et la plus droite. b. Une ligne en rotation partielle donne un triangle.
|
|
|
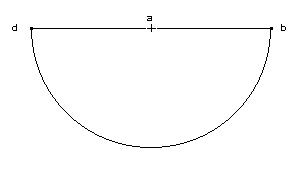
c. Une ligne en rotation complète donne un cercle. d. Un demi cercle en rotation sur son diamètre donne une sphère. Conclusion : l’infini est triangle, cercle et sphère.
|
|
3. La ligne infinie est le triangle maximum : démonstration par le nombre de côtés.
a. Il n’y a qu’un maximum infini unique.
b. La somme de deux côtés d’un triangle est supérieure au troisième côté (ab + bc > ac).
c. Une partie de l’infini est infinie. Si un côté est infini, alors les deux autres le sont aussi.
d. Il n’y a qu’un infini (Cf. 3a). Donc, le triangle infini n’a qu’une ligne infinie.
e. Le triangle infini est le plus vrai. Donc, il a trois côtés et la ligne infinie est une en trois.
f. De même pour les angles.
Conclusion : ligne infinie et angle infini sont la même chose.
4. La ligne infinie est le triangle maximum : démonstration par la mesure des angles.
|
a. La somme des angles d’un triangle est égale à deux droits. Donc, plus un angle augmente, plus les autres diminuent. b. Un triangle dont un angle fait 180° a un seul angle qui en fait trois. (Cf.3f) c. La somme de deux côtés d’un triangle est d’autant supérieure au troisième côté que leur angle est aigu. d. Corollaire : plus l’angle est obtus, plus la somme des deux côtés égale le troisième côté. (la surface diminue). Conclusion : La ligne infinie est le triangle maximum. |
|
5. Le triangle maximum est un cercle :
|
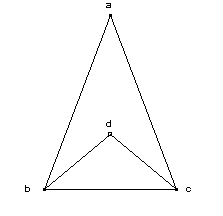
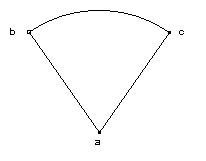
a. Une ligne ab donne par rotation un triangle abc. Si ab est infinie, elle donne par rotation complète un cercle infini. b. La portion de l’arc bc est une ligne droite. (Cf. 1a) c. Une partie de l’infini est infinie. Donc, bc est la circonférence du cercle maximum. (Cf. 1a) d. Donc le triangle abc est le cercle maximum. e. bc est une ligne droite. Donc, ab n’est pas plus grande que bc. (Cf. 2a) f. Il ne peut y avoir deux infinis (Cf. 3a). Donc, ab et bc sont une seule ligne. Conclusion : la ligne infinie est un triangle et est un cercle. |
|
6. La ligne infinie est une sphère :
a. ab est la circonférence du cercle maximum (Cf.5f).
b. ab a donné le triangle abc (Cf.5a).
c. bc est la ligne infinie et est le cercle maximum. (Cf.conclusion 5)
d. Donc, ab est revenu en c par un retour complet sur elle-même.
e. Le cercle infini donne, par retour sur lui, une sphère.
Conclusion : abc est un cercle, est un triangle, est une ligne infinie (Cf. conclusion 5) et est une sphère. C.Q.F.D.
Malgré les apparences de raisonnement, on a plus affaire à des descriptions intuitives qu’à de véritables démonstrations. C’est pourquoi il est tout à fait illusoire de ne se fier qu’à ce texte pour se donner une image des mathématiques cusaines. Il faut lire les textes proprement mathématiques pour y rencontrer Nicolas de Cues mathématicien.