Le minimum
Le texte De la perfection mathématique, date de 1458 et est adressé à Antoine de la Cerda. N. de Cues considérait cet ouvrage comme son meilleur traité mathématique, un peu comme le point d’orgue de sa recherche. Le début expose clairement la nouvelle méthode :
Mon but est d’arriver à la perfection mathématique par la coïncidence des opposés. Et parce que cette perfection consiste pour tout dans l’égalité en quantité de la droite et de la courbe, je propose de chercher le rapport de deux lignes droites se tenant dans le rapport de la corde à son arc : connaissant ce rapport, j’obtiens un moyen d’égaliser la quantité courbe avec la droite .
On part de la coïncidence de l’arc le plus petit et de la corde la plus petite, aperçue par une vision intellectuelle, puis on utilise ce rapport dans les grandeurs intermédiaires.
|
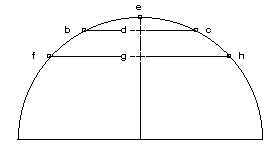
De fait, plus la corde est petite, d’autant la flèche est plus petite. Comme la flèche de de la corde bc est plus petite que la flèche ge de la corde fh, parce que bc est plus petite que fh, et ainsi de suite.
|
|
Donc, la plus petite corde telle qu’on ne peut en donner de plus petite, si elle était assignable, n’aurait pas de flèche, et ainsi ne pourrait être plus petite que son arc. Il y aurait donc là coïncidence de la corde et de l’arc, si on en arrivait à leur quantité minimale. Il est nécessaire que l’intellect voie cela tout à fait et il lui est permis de le savoir : ni l’arc ni la corde - en tant que quantités - ne peuvent être simplement les plus petits en acte et en puissance, puisque le continu est toujours divisible. Pour parvenir à la connaissance de leur rapport, je me tourne vers la vision intellectuelle, et je dis que je vois où est l’égalité de la corde et de l’arc, à savoir simplement dans le minimum de chacun des deux. A partir de cette égalité entrevue, je poursuis la recherche visée au moyen d’un triangle rectangle, et par la proposition qui suit...(p. 433-435)
La vision intellectuelle est une certitude métaphysique : elle instaure une nécessité en essence. Elle abroge la notion de quantité au profit de l’idée d’égalité des grandeurs. Elle porte sur des grandeurs absolues, en maximum et en minimum, au-delà de la mesure quantitative, sur des figures insensibles et parfaites. Elle ne fait plus la différence entre le petit et le grand, puisque le minimum et le maximum sont vus « pareillement ». Dans le sensible, le petit et le grand sont relatifs et sont comparables, donc mesurables. Dans l’insensible absolu, il n’y a ni augmentation, ni diminution. Il suffit alors de s’appuyer sur les propriétés de ces deux extrêmes que sont le minimum et le maximum pour en déduire les propriétés des dimensions intermédiaires.
Dans cette coïncidence de l’arc minimal et de la corde minimale, l’opposition disparaît. La différence ne se réduit pas à un point, sorte d’atome subsistant entre les deux, mais il n’y a plus de flèche (minima chorda … non haberet sagittam). La coïncidence débute sur un rien, puis, lorsque les deux lignes se séparent pour former un arc et une corde, alors, la flèche qui fait la différence, réapparaît.
La proposition principale se résume ainsi :
|
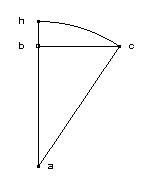
demi-arc / demi-corde = 3 rayons / (2 rayons + (rayon-flèche)). On dessine un quadrant de cercle. hc est le demi-arc ; bc est la demi-corde ; ac et ah sont des rayons. Le rapport de hc à bc est comme celui de trois rayons à deux rayons plus ab. |
|
|
N. de Cues montre que la même relation existe dans le minimum (l’arc le plus petit) comme dans le maximum (c’est-à-dire le quart de cercle). Il considère donc qu’elle existe dans toutes les positions intermédiaires. Il en tire des applications (convertir un arc en droite, convertir une droite en arc), et des corollaires :
Mais les diverses propositions qu’il déduit à la fin de l’ouvrage sont souvent fausses. |